Frações

    O símbolo 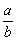 significa a:b, sendo a e b números naturais e b diferente de zero.

    Chamamos:

      de fração;

     a de numerador;

     b de denominador.

    Se a é múltiplo de b, então 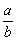 é um número natural.

    Veja um exemplo:

    A fração 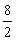 é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim,  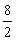é um número natural e 8 é múltiplo de 2.

    Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.

Vamos la crianças ?

Equação do segundo grau

Progressões: exemplo de uma P.A. e uma P.G

Progressões: Aprenda as diferenças de P.A. e P.G.

Progressões: exemplo de uma P.A. e uma P.G

1) Progressões Aritméticas:

Definição: P.A são sequências de números, em que a diferença entre um número e seu antecedente é igual à uma razão “r”. Elas podem ser crescentes ou decrescentes. Nas progressões crescentes, a razão será positiva, e nas decrescentes, será negativa.

O valor da razão “r” será calculado da seguinte forma:

r = a2 – a1 ou r = a3 – a2 ou r = a4 – a3 ou r = a5 – a4 ou r = a6 – a5, e assim por diante.

Nos exercícios de progressões aritméticas (P.A.), devemos ter em mente duas fórmulas:

a) N-ésimo termo de uma P.A.:

A fórmula abaixo é usada quando se quer determinar o n-ésimo termo de uma progressão aritmética.

an = a1 + (n – 1) . r

Onde,

an = n-ésimo termo que se quer determinar.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

r = razão da sequência, encontrado pela diferença de um termo e seu antecessor.

Exercício:

Dada a sequência (1,3,5,7,9,11,13,15,17), calcule o décimo oitavo termo dessa sequência.

a1 = 1

n = 18

r = 3 -1 = 2   ou   r = 5 – 3 = 2    ou   r = 7 – 5 = 2

a18 = ?

an = a1 + (n – 1) . r

a18 = 1 + (18-1) . 2

a18 = 1 + 17.2

a18 = 1 + 34

a18 = 35

b) Soma dos n primeiros termos:

Podemos fazer a soma de n termos de uma progressão aritmética por meio de uma fórmula, que será:

Sn = ((a1 + an) . n) / 2

Sn = soma dos n termos

a1 = primeiro termo da sequência.

an = n-ésimo termo da sequência.

n = número de termos da sequência.

Exercício:

Dada a sequência (1,3,5,7,9,11,13,15,17), calcule a soma dos termos dessa P.A.

a1 = 1

an = 17

n = 9

Sn = ?

Sn = ((a1 + an) . n) / 2

Sn = ((1 + 17) . 9) / 2

Sn = (18.9) / 2

Sn = 81

2) Progressões Geométricas:

Definição: P.G. são sequência de números, em que a divisão entre um número e seu antecedente é igual à uma razão “q”. Elas podem ser crescentes ou decrescentes. Nas progressões crescentes, o q será maior que 1, e nas progressões decrescentes, será menor que 1 e maior do que zero. Nas progressões com razão negativa, a sequência não será nem crescente nem decrescente.

O valor da razão “q” será calculado da seguinte forma:

q = a2 / a1 ou q = a3 / a2 ou q = a4 / a3 ou q = a5 / a4 ou q = a6 / a5, e assim por diante.

Nos exercícios de progressões geométricas (P.G.), devemos ter em mente três fórmulas:

a) N-ésimo termo de uma P.G.:

A fórmula abaixo é usada quando se quer determinar o n-ésimo termo de uma progressão geométrica.

an = a1 . q  ^ (n – 1)

Onde,

an = n-ésimo termo que se quer determinar.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1,2,4,8,16,32,64,128,256), calcule o décimo oitavo termo dessa sequência.

a1 = 1

q = 2 / 1 = 2    ou    q = 4 / 2 = 2    ou   q = 8 / 4 = 2    ou    q = 16 / 8 = 2

n = 18

an = ?

an = a1 . q  ^ (n – 1)

a18 = 1 . 2 ^ (18 – 1)

a18 = 1 . 2  ^ 17

a18 = 1 . 131072

a18 = 131072

b) Soma dos n primeiros termos (P.G. finita):

Podemos fazer a soma de n termos de uma progressão geométrica por meio de uma fórmula, que será:

Sn = (a1 . ((q ^ n) – 1)) / (q – 1)

Onde,

Sn = soma dos n primeiros termos.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1,2,4,8,16,32,64,128,256), calcule a soma dos n termos dessa sequência.

a1 = 1

n = 9

q = 2 / 1 = 2    ou    q = 4 / 2 = 2    ou   q = 8 / 4 = 2    ou    q = 16 / 8 = 2

Sn = ?

Sn = (a1 . ((q ^ n) – 1)) / (q – 1)

Sn = (1 . ((2 ^ 9) – 1 ) / (2-1)

Sn = (1. (512) – 1) / (1)

Sn = (512 – 1) / 1

Sn = 511

c) Soma dos infinitos termos de uma sequência (P.G. infinita):

Podemos fazer a soma de infinitos termos de uma progressão geométrica por meio de uma fórmula, que será:

S infintos = a1 / (1 – q)

Observação: Nesse caso específico, a razão deve estar compreendida entre -1 e 1 (condição necessária para usar a equação abaixo).

Onde,

S infinitos = soma dos infinitos termos.

a1 = primeiro termo da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1, 0.5, 0.25, 0.125, …), calcule a soma dos infinitos termos dessa sequência.

Observe o sinal de “…”, indicando que a P.G. é infinita.

a1 = 1

q = 0,5 / 1 = 0,5   ou    q = 0.25 / 0.5 = 0.5    ou   q = 0.125 / 0.25 = 0.5

S infintos = a1 / (1 – q)

S infintos = 1 / (1 – 0,5)

S infinitos = 1 / 0,5

S infinitos = 2

As fórmulas das progressões aritmética e geométrica devem ser memorizadas por aquelas pessoas que irão fazer provas de matemática ou raciocínio lógico, pois a grande maioria dessas provas cobram assuntos relacionados à progressões.