Frações

    O símbolo 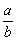 significa a:b, sendo a e b números naturais e b diferente de zero.

    Chamamos:

      de fração;

     a de numerador;

     b de denominador.

    Se a é múltiplo de b, então 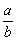 é um número natural.

    Veja um exemplo:

    A fração 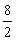 é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim,  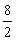é um número natural e 8 é múltiplo de 2.

    Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.

Vamos la crianças ?

Equação do segundo grau

Progressões: exemplo de uma P.A. e uma P.G

Progressões: Aprenda as diferenças de P.A. e P.G.

Progressões: exemplo de uma P.A. e uma P.G

1) Progressões Aritméticas:

Definição: P.A são sequências de números, em que a diferença entre um número e seu antecedente é igual à uma razão “r”. Elas podem ser crescentes ou decrescentes. Nas progressões crescentes, a razão será positiva, e nas decrescentes, será negativa.

O valor da razão “r” será calculado da seguinte forma:

r = a2 – a1 ou r = a3 – a2 ou r = a4 – a3 ou r = a5 – a4 ou r = a6 – a5, e assim por diante.

Nos exercícios de progressões aritméticas (P.A.), devemos ter em mente duas fórmulas:

a) N-ésimo termo de uma P.A.:

A fórmula abaixo é usada quando se quer determinar o n-ésimo termo de uma progressão aritmética.

an = a1 + (n – 1) . r

Onde,

an = n-ésimo termo que se quer determinar.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

r = razão da sequência, encontrado pela diferença de um termo e seu antecessor.

Exercício:

Dada a sequência (1,3,5,7,9,11,13,15,17), calcule o décimo oitavo termo dessa sequência.

a1 = 1

n = 18

r = 3 -1 = 2   ou   r = 5 – 3 = 2    ou   r = 7 – 5 = 2

a18 = ?

an = a1 + (n – 1) . r

a18 = 1 + (18-1) . 2

a18 = 1 + 17.2

a18 = 1 + 34

a18 = 35

b) Soma dos n primeiros termos:

Podemos fazer a soma de n termos de uma progressão aritmética por meio de uma fórmula, que será:

Sn = ((a1 + an) . n) / 2

Sn = soma dos n termos

a1 = primeiro termo da sequência.

an = n-ésimo termo da sequência.

n = número de termos da sequência.

Exercício:

Dada a sequência (1,3,5,7,9,11,13,15,17), calcule a soma dos termos dessa P.A.

a1 = 1

an = 17

n = 9

Sn = ?

Sn = ((a1 + an) . n) / 2

Sn = ((1 + 17) . 9) / 2

Sn = (18.9) / 2

Sn = 81

2) Progressões Geométricas:

Definição: P.G. são sequência de números, em que a divisão entre um número e seu antecedente é igual à uma razão “q”. Elas podem ser crescentes ou decrescentes. Nas progressões crescentes, o q será maior que 1, e nas progressões decrescentes, será menor que 1 e maior do que zero. Nas progressões com razão negativa, a sequência não será nem crescente nem decrescente.

O valor da razão “q” será calculado da seguinte forma:

q = a2 / a1 ou q = a3 / a2 ou q = a4 / a3 ou q = a5 / a4 ou q = a6 / a5, e assim por diante.

Nos exercícios de progressões geométricas (P.G.), devemos ter em mente três fórmulas:

a) N-ésimo termo de uma P.G.:

A fórmula abaixo é usada quando se quer determinar o n-ésimo termo de uma progressão geométrica.

an = a1 . q  ^ (n – 1)

Onde,

an = n-ésimo termo que se quer determinar.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1,2,4,8,16,32,64,128,256), calcule o décimo oitavo termo dessa sequência.

a1 = 1

q = 2 / 1 = 2    ou    q = 4 / 2 = 2    ou   q = 8 / 4 = 2    ou    q = 16 / 8 = 2

n = 18

an = ?

an = a1 . q  ^ (n – 1)

a18 = 1 . 2 ^ (18 – 1)

a18 = 1 . 2  ^ 17

a18 = 1 . 131072

a18 = 131072

b) Soma dos n primeiros termos (P.G. finita):

Podemos fazer a soma de n termos de uma progressão geométrica por meio de uma fórmula, que será:

Sn = (a1 . ((q ^ n) – 1)) / (q – 1)

Onde,

Sn = soma dos n primeiros termos.

a1 = primeiro termo da sequência.

n = número de termos da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1,2,4,8,16,32,64,128,256), calcule a soma dos n termos dessa sequência.

a1 = 1

n = 9

q = 2 / 1 = 2    ou    q = 4 / 2 = 2    ou   q = 8 / 4 = 2    ou    q = 16 / 8 = 2

Sn = ?

Sn = (a1 . ((q ^ n) – 1)) / (q – 1)

Sn = (1 . ((2 ^ 9) – 1 ) / (2-1)

Sn = (1. (512) – 1) / (1)

Sn = (512 – 1) / 1

Sn = 511

c) Soma dos infinitos termos de uma sequência (P.G. infinita):

Podemos fazer a soma de infinitos termos de uma progressão geométrica por meio de uma fórmula, que será:

S infintos = a1 / (1 – q)

Observação: Nesse caso específico, a razão deve estar compreendida entre -1 e 1 (condição necessária para usar a equação abaixo).

Onde,

S infinitos = soma dos infinitos termos.

a1 = primeiro termo da sequência.

q = razão da sequência, encontrado pela divisão de um termo e seu antecessor.

Exercício:

Dada a sequência (1, 0.5, 0.25, 0.125, …), calcule a soma dos infinitos termos dessa sequência.

Observe o sinal de “…”, indicando que a P.G. é infinita.

a1 = 1

q = 0,5 / 1 = 0,5   ou    q = 0.25 / 0.5 = 0.5    ou   q = 0.125 / 0.25 = 0.5

S infintos = a1 / (1 – q)

S infintos = 1 / (1 – 0,5)

S infinitos = 1 / 0,5

S infinitos = 2

As fórmulas das progressões aritmética e geométrica devem ser memorizadas por aquelas pessoas que irão fazer provas de matemática ou raciocínio lógico, pois a grande maioria dessas provas cobram assuntos relacionados à progressões.

P.A e P.G

EQUAÇÃO DO 2º GRAU

Uma equação é uma expressão matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas. Veja:

• 2x + 1 = 0. O expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
• 2x² + 2x + 6 = 0. Há duas incógnitas x nessa equação, e uma delas possui expoente 2. Essa equação é classificada como do 2º grau.
• x³ – x² + 2x – 4 = 0. Nesse caso, temos três incógnitas x, e o maior expoente – no caso, expoente 3 – torna a equação como do 3º grau.

O que são raízes ou soluções de uma equação do 2º grau?

Cada modelo de equação possui uma forma de resolução. Trabalharemos a forma de resolução de uma equação do 2º grau por meio do método de Bhaskara . Determinar a solução de uma equação é o mesmo que descobrir suas raízes, isto é, o valor ou os valores que satisfazem a equação. As raízes da equação do 2º grau x² – 10x + 24 = 0, por exemplo, são x = 4 ou x = 6, pois:

Substituindo x = 4 na equação, temos:

x² – 10x + 24 = 0
4² – 10 * 4 + 24 = 0
16 – 40 + 24 = 0
–24 + 24 = 0
0 = 0 (verdadeiro)

Substituindo x = 6 na equação, temos:

x² – 10x + 24 = 0
6² – 10 * 6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0
0 = 0 (verdadeiro)

Podemos verificar que os dois valores satisfazem a equação, mas como podemos determinar os valores que tornam a equação uma sentença verdadeira? É essa forma de determinar os valores desconhecidos que abordaremos a seguir.

Método de Bhaskara

Vamos determinar pelo método resolutivo de Bhaskara os valores da seguinteequação do 2º grau: x² – 2x – 3 = 0.

Uma equação do 2º grau possui a seguinte lei de formação: ax² + bx + c = 0, em que a, b e c são os coeficientes. Portanto, os coeficientes da equação x² – 2x – 3 = 0 são a = 1, b = –2 e c = –3.

Na fórmula de Bhaskara, utilizaremos somente os coeficientes. Veja:

1º passo: determinar o valor do discriminante ou delta (∆)

∆ = b² – 4 * a * c
∆ = (–2)² – 4 * 1 * (–3)
∆ = 4 + 12
∆ = 16

2º passo:

x = – b ± √∆
      2∙a

x = –(– 2) ± √16
       2∙1

x = 2 ± 4
     2

x' = 2 + 4 = 6 = 3
   2       2

x'' = 2 – 4 = – 2 = – 1
2        2

Os resultados são x’ = 3 e x” = –1.

Exemplo II: Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.

Os coeficientes são:

a = 1
b = 8
c = 16

∆ = b² – 4 * a * c
∆ = 8² – 4 * 1 * 16
∆ = 64 – 64
∆ = 0

x = – b ± √∆
     2∙a

x = – 8 ± √0
     2∙1

x' = x'' = –8 = – 4
    2

No exemplo 2, devemos observar que o valor do discriminante é igual a zero. Nesses casos, a equação possuirá somente uma solução ou raiz única.

Exemplo III: Calcule o conjunto solução da equação 10x² + 6x + 10 = 0, considerada de 2º grau.

∆ = b² – 4 * a * c
∆ = 6² – 4 * 10 * 10
∆ = 36 – 400
∆ = –364

Nas resoluções em que o valor do discriminante é menor que zero, isto é, o número é negativo, a equação não possui raízes reais

Eu mudaria o sinal então ficaria o sinal de menos e moveria para o seis então ficaria 8 - 4 = 4

O gráfico do amor

Um dia, vivi um amor! Gostoso, atencioso, caloroso... A intensa necessidade de estar era notória, Meu amor aumentava, e sua correspondência também... Muito mais do que a minha, ... As manhãs eram gostosas, As tardes eram alegres, e As noites? quentes...ah... E o tempo passando... Meu amor foi crescente... Situado ao primeiro quadrante... Sem defeitos, sem tristezas... Tendia ao infinito por vontade... Mas existe amor eterno? Será que cresceria eternamente? Existe um tempo, onde uma causa... Imperdoável causa esta, que nos entristece.. Que leva ao tombo, ao fim, ou ao intervalo? Esperança minha que seja um intervalo... Mas que grande intervalo... Retrógrado, para partir do mesmo ponto.. Para recomeçar com a mesma intensidade... Mas o infinito existe, existe o para sempre? Ou o infinito é um pensamento imaginário... Desejoso e necessário ao coração, às emoções... O crescer pode até não ser infinito, Mas sonho com a tranqüilidade, com a bonança... Com o equilíbrio das emoções... Ainda sonho com o meu amor... Quem sabe voltando para mim.... June Cunha de Araujo

Um jeito diferente e criativo de aprender a tabuada

Tabuada sempre foi um pesadelo tanto para as crianças como para seus pais. Outro dia, recebi uma carta de uma mãe preocupadíssima porque seu filho não conseguia decorar a tabuada. Enquanto lia as aflições dessa senhora, lembrei-me de um novo amigo, doutor Rubens, médico ortopedista, que nas poucas horas vagas de que dispõe ajuda sobrinhos e filhos a resolver as questões na Aritmética. Foi ele quem me contou que numa dessas sessões de auxílio matemático conseguiu demonstrar ao filho que quem conhece as tabuadas do 2 e do 3 já sabe um bom pedaço de todas as outras. 

Basta aplicar o fato, curioso para as crianças, de que as multiplicações2 x 9 e 3 x 9 , 2 x 8 e 3 x 8, 2 x 7, 3 x 7 etc., dão os mesmos resultados das multiplicações 9 x 2 e 9 x 3, 8 x 2 e 8 x 3, 7 x 2 e 7 x 3. Essa propriedade de poder “comutar” a ordem dos fatores sem que, com isso, se modifique o resultado de uma multiplicação, embora simples ou, talvez, exatamente por isso, acaba se tornando um poderoso auxiliar no agradável jogo de brincar com os números. 
Fiquei duplamente contente. Primeiro porque o Rubens deu um jeito na minha coluna vertebral e segundo porque, mesmo sem saber, acabou ajudando esta coluna, o “Dois mais Dois”, ao revelar a este velho professor que ainda existem pais e tios preocupados com o lúdico da Aritmética no contato com os filhos e sobrinhos. Quanto à mãe aflita com a tabuada do filho, o caso me pareceu mais sério, pois o menino ia bem até a tabuada do 5, mas do 6 ao 9 era um terror. Tranqüilizei-a e sugeri que ela brincasse com o menino usando um processo do qual ainda se encontram vestígios na Índia, no Iraque, no centro da França, norte da África, etc. 
Então, vamos lá e mãos ao alto. Não se assuste, não é um assalto, apenas um jeito novo e diferente de aprender as tabuadas do 6 ao 9. Exemplo: 7 x 9. Levante as mãos. Depois, escolha uma delas, dobre os dedos correspondentes à quantidade em que o 7 excede o 5, isto é, 2. 
Faça o mesmo com a outra mão para 9, isto é, dobre os dedos correspondentes á quantidade que o 9 excede o 5. Ou seja, 4. 
Responda quantos dedos estão dobrados. Seis. Ok? Dois em uma (7-5) e quatro na outra (9-5). Pois bem, a soma dos dedos dobrados (6) responde à dezena (60) do resultado. Assim (2 + 4) x 10 = 60. Logo, descobrirmos a dezena da multiplicação de 7 por 9, 7 x 9 = sessenta e ??? Para descobrirmos as unidades, basta contarmos os dedos levantados nas duas mãos (3 numa e 1na outra) e multiplicarmos esses números: 3 x 1 = 3 
(2+4) dedos dobrados = 60 
Logo, 7 x 9 = 63 
(3x1) dedos levantados = 3 
Agora, tente você. Faça 8 x 6 e vamos conferir: 
8 x 6 = 48 
Dobrados: 8 – 5 = 3; 6 - 5 = 1, (3 + 1) x 10 = 40 
Levantados: 2 4, 2 x 4 = 8 
Resultado: = 48 
Daqui para a frente é com você, tente outros e veja que a técnica não é complicada. Aliás, vários livros contam a história dessa interessante maneira de multiplicar. Um deles, recentemente traduzido para o português, é Os números, de Georges Ifrah. Se você brincar bastante, vai ter uma surpresa ao fazer 6 x 7. Verá somente 3 dedos dobrados. Não se preocupe, não está errado, pois terá levantado 4 dedos numa das mãos e 3na outra, logo 6 x 7 resulta 30 e 12 (3x4), ou seja, 42. 
Observe, por exemplo, como os franceses dizem 80: é quatre vingt, ou quatro vintes, que significa 4 vezes 20 ou o nosso 80. Isso pode ter tido origem no calculista da aldeia dos irresistíveis gauleses Asterix, Obelix e companhia. Ele talvez usasse os dedos das mãos e dos pés para contar, construindo assim um sistema de numeração de base 20. Os vestígios teriam sobrevivido no modo como os franceses dizem 80. Mas isso é outra história. Mãos ao alto e vamos treinar a tabuada.